42 - Lugares Geométricos - Matemática - Vestibulando Digital

Jogos matemáticos - 42

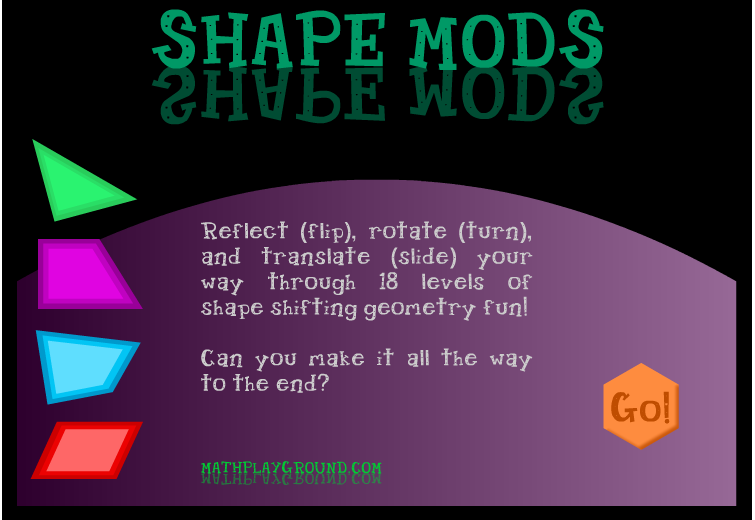
SHAPE MODS

Este jogo é uma excelente oportunidade para você treinar ou mesmo aprender um tópico muito importante: as transformações geométricas!
Clique e comece a compreender melhor os conceitos de reflexão, translação, rotação e espelhamento.

SHAPE MODS

O Legado de Pitágoras - 03 - Desafiando Pitágoras

*BOLYAI

János Bolyai

Data de Nascimento: 15 de dezembro, 1802 Kolozsvár , Hungria ( agora Cluj , Roménia)
Morreu em: 27 de janeiro de 1860 Marosvásárhely , Hungria ( agora Tirgu - Mures, Roménia)

Os pais de János Bolyai foram Zsuzsanna Benkö , de Kolozsvár e Farkas Bolyai , de Bolya (perto Nagyszeben ) . János nasceu em Zsuzsanna da casa dos pais em Kolozsvár ( agora renomeada Cluj , na Roménia ), mas logo foi para Marosvásárhely onde seu pai Farkas tinha um trabalho para os calvinistas universitários de ensino de matemática , física e química . Farkas Bolyai sempre quis seu filho para ser um matemático , e ele trouxe -lo com isso em mente. Pode-se supor que isto significaria que a educação de János foi colocado pela primeira vez na casa Bolyai , mas não foi assim para Farkas acredita-se que uma mente sã só poderia conseguir grandes coisas se fosse em um corpo saudável som , eu sei que em seus primeiros anos mais foi dada atenção ao desenvolvimento físico do János . Ficou claro desde o início , no entanto, János Isso era uma criança extremamente inteligente e atento [7] : -

... Quando ele tinha quatro anos ele poderia distinguir certas figuras geométricas , sabia sobre a função seno , e pode identificar as melhores constelações conhecidas. Até o momento ele tinha cinco anos [ ele ] tinha - aprendido, praticamente sozinho, para ler. Ele estava bem acima da média em línguas e música de aprendizagem. Com a idade de sete anos ele assumiu a tocar violino e os progressos realizados mais disponível que ele foi logo tocando peças de concerto difíceis.

É importante compreender que, embora Farkas tinha um post palestras que ele não estava bem pagos e até mesmo Embora ele ganhou dinheiro extra a partir de uma variedade de fontes diferentes , János ainda foi trazido em condições financeiras ruins. Também a mãe de János era uma pessoa bastante difícil ea casa não era um lugar particularmente feliz para o menino crescer.

Até János tinha nove anos os melhores alunos do Colégio Marosvásárhely ensinou-lhe todas as disciplinas escolares habituais , exceto matemática, que ele foi ensinado por seu pai. Somente a partir de nove anos de idade ele frequentar a escola. Até o momento Bolyai tinha 13 anos, ele tinha dominado os cálculos e outras formas de mecânica analítica , o seu pai continua a dar-lhe instruções . Por esta altura, no entanto , ele estava freqüentando o Colégio Calvinista em Marosvásárhely Apesar de ter começado no quarto ano e frequentou aulas muitas vezes destinados para os alunos seniores.

Em 1816, Farkas escreveu a Gauss Seu amigo perguntando se ele iria deixar János viver com ele e levá-lo como aluno eu sei que ele pode receber a melhor educação possível matemática. Certamente teria sido uma educação maravilhosa para János e é interessante especular que benefícios pode ter como para o mundo da matemática, se ele tivesse aceitado o plano. Gauss No entanto, rejeitou a idéia. Quando János formou na faculdade Marosvásárhely em 30 de junho de 1817 não estava claro como ele poderia conseguir uma boa educação matemática . Nenhuma das universidades em Pest ou Viena oferecidas de boa qualidade da educação matemática , neste momento, e Farkas não podia dar ao luxo de enviar seu filho para eles a mais prestigiosa universidade no exterior. Os János decisão de que iria estudar engenharia militar na Academia de Engenharia em Viena não foi tomada sem muita dor de cabeça e busca da alma , mas no final desta rota foi escolhida como a menos má das opções. Isso não quer dizer que a Academia não o fez sobressair no ensino da matemática , pois na verdade o assunto foi Salientou Durante todo o curso . János permaneceu por mais um ano no Colégio Marosvásárhely tentativa de ganhar a entrada para a Academia em Viena, ao mais alto nível possível, que ele alcançou.

Ele estudou no Royal Faculdade de Engenharia , em Viena 1818-1822 concluir o curso de sete anos em quatro anos. Ele era um estudante excepcional e de seu segundo ano de estudo, ele veio por cima na maioria dos temas que estudou. Além disso, ele teve tempo para se tornar um excelente desportista, e ele continuou a tomar o seu violino a sério e executada enquanto em Viena. Sua mãe morreu em 18 setembro de 1821 , mas ele foi capaz de continuar seus estudos. Quando ele se formou na Academia em 6 de setembro de 1822 ele teve mais disponível Alcançados notável sucesso que ele passou mais um ano em Viena, em estudos acadêmicos antes de entrar no serviço militar. Claro que ele tinha recebido treinamento militar durante o seu tempo em Viena , para os meses de verão foram dedicadas a isso, mas a natureza de Bolyai não lhe permitia aceitar facilmente a rigorosa disciplina militar.

Em setembro de 1823 Entrou no corpo de engenharia do exército como um subtenente e foi enviado para trabalhar em fortificações no Temesvár . Ele gastou um total de 11 anos no serviço militar e tinha a fama de ser o melhor espadachim e dançarina do Exército Imperial Austro -Húngaro. Ele não fumava nem bebia , nem mesmo café, e com a idade de 23 , ele foi relatado para ainda manter a modéstia de inocência. Ele também era um poliglota que fala nove línguas , incluindo chinês e tibetano.

Por volta de 1820 , quando ele ainda estava estudando em Viena, Bolyai começou a seguir o mesmo caminho que seu pai tinha tomado na tentativa de substituir o axioma das paralelas de Euclides com um outro axioma que poderia ser deduzida a partir das outras. Na verdade, ele deu -se esta abordagem para ainda Dentro de um ano , em 1820, como Seus cadernos mostram agora, ele começou a desenvolver as idéias básicas da geometria hiperbólica . Em 03 de novembro de 1823 , ele escreveu a seu pai que ele teve: -

... criou um novo , um outro mundo a partir do nada ...

mas ele ainda acrescentou algumas linhas mais tarde que não foi criado ainda. Por volta de 1824 No entanto, há evidências que sugerem que ele tinha desenvolvido mais do que deveria aparecer em seu tratado como um sistema completo de geometria não-euclidiana . No início de 1825 Bolyai viajou para Marosvásárhely e explicou suas descobertas a seu pai. No entanto Farkas Bolyai não reagiu com entusiasmo o que claramente desapontado János . Bolyai foi enviada para Arad em 1826 e lá encontrou Wolther que o Capitão von Eckwehr , um de seus antigos professores de matemática da Academia de Viena , também estava estacionado . Bolyai deu-lhe um projecto de materiais que ele estava escrevendo sobre a teoria da geometria , pois , provavelmente, esperava alguns comentários construtivos dele. No entanto, afigura-se de escritos posteriores de Bolyai Que ele não tem nada de von Eckwehr , em particular, ele nunca recebeu o manuscrito de volta.

Em 1830, Bolyai - aprendi que ele estava a ser enviado para uma postagem em Lemberg . No início de 1831 , ele partiu para Lemberg , mas visitou o Seu Pai em Marosvásárhely em seu caminho . Até agora Farkas tinha chegado a compreender o significado completo do que o seu filho tinha feito e fortemente encorajou a escrever o trabalho para publicação como um anexo à Tentamen que estava perto de publicação. Bolyai escreveu mais tarde: -

Se meu pai não aconteceu para exortar ou mesmo forçar-me a Marosvásárhely , na minha maneira de dever em Lemberg , imediatamente a colocar as coisas no papel, possivelmente, o conteúdo do Anexo nunca teria visto a luz do dia .

O que estava contido nesta obra-prima matemática ? Depois de configurar suas próprias definições de " paralelo" e mostrar que se o quinto postulado realizada em uma região do espaço realizada todo , e vice- versa , então ele declarou claramente os diferentes sistemas que iria considerar: -

... denotamos por Σ um sistema de geometria com base na hipótese de que o quinto postulado de Euclides é verdade, e S pelo sistema com base na hipótese contrária. Todos os teoremas estávamos sem Especificando o sistema Σ ou S em que o teorema é válido se destinam a ser absoluta , isto é, válida independentemente de Σ ou S é verdade.

Hoje chamamos Estes três geometrias euclidiana , hiperbólica e absoluta. A maioria das apêndice aborda geometria absoluta. Até 20 de Junho de 1831, o Anexo tinha sido publicado naquele dia para Farkas Bolyai enviou para reimprimir a Gauss que , ao ler o Apêndice , escreveu a um amigo dizendo : -

Eu considero este jovem geômetra Bolyai como um gênio de primeira ordem .

Para Farkas Bolyai , no entanto , Gauss escreveu: -

Elogiá-lo equivaleria a me elogiar . Para a totalidade do conteúdo do trabalho ... coincide quase exatamente com as minhas próprias meditações que ocuparam minha mente durante os últimos trinta ou 35 anos .

Não há dúvida de que Gauss estava simplesmente declarando fatos aqui . A referência mais clara nas cartas de Gauss à Sua obra sobre a geometria não-euclidiana , que mostra a profundidade de sua compreensão , ocorre em uma carta que ele escreveu para Taurinus em 08 de novembro de 1824 , quando ele escreveu : -

A suposição de que a soma dos três ângulos de um triângulo é menor do que 180 ° leva a uma geometria curioso , bastante diferente do nosso [isto Geometria euclidiana ] mas completamente consistente, o que eu tenho desenvolvido para toda a minha satisfação , eu sei que posso resolver todos os problemas nele com exceção da determinação de uma constante, o que não pode ser fixado a priori. .... os três ângulos de um triângulo ser tão pequena quanto se queira , se apenas os lados são tomados suficientemente grande, no entanto, a área do triângulo nunca pode ser superior a , ou até se atingir um certo limite, independentemente de quão grande é os lados são .

Bolyai não permanecem por muito tempo em Lemberg , em 1832, ele foi enviado a Olmutz onde ele agora era um capitão . A descoberta de que Gauss tinha antecipado muito do seu trabalho , no entanto, muito chateado Bolyai que tomou isso como um duro golpe . Ele ficou irritado e uma pessoa difícil de obter com . Começou a sua saúde se deteriorou e ele foi atormentado por uma febre que freqüentemente desativado ele para que ele achou cada vez mais difícil de realizar seus deveres militares . Aposentou-se em 16 de junho de 1833, pedindo para ser aposentada , e por um curto período de tempo foi morar com o pai.

Depois de passar um tempo com seu pai , Bolyai foi morar na propriedade da família em Domald que a família tinha herdado da mãe de Farkas Bolyai . Ele havia conhecido Rozália Kibédi Orbán e viveram juntos na Domald de 1834. Eles não se casar, no entanto , desde que a lei insistia em dinheiro a ser depositado antes de um casamento pode ter lugar e Bolyai não poderia arcar com o dinheiro. Ele teve dois filhos com Rozália mas sua pensão era insuficiente para permitir que a família viver com conforto . Ele não parece ter conseguido bem o dinheiro que ele tinha normal ter mantido a propriedade em boas condições. Parece que Farkas Bolyai não aprovava Rozália , estava descontente com a situação financeira de seu filho, foi infeliz Que a propriedade da família em Domald não estava sendo bem cuidada , e foi infeliz que seu filho estava prejudicando o seu bom nome para Farkas foi altamente membro respeitado da comunidade.

Certamente Bolyai continuou a desenvolver teorias matemáticas , enquanto ele vivia em Domald , mas estar isolado do resto do mundo da matemática muito do que ele tentou foi de pouco valor. Sua única grande empresa , para tentar desenvolver toda a matemática com base em sistemas axiomáticos , foi iniciado em 1834, para que ele escreveu no prefácio Naquele ano, mas ele nunca concluiu o trabalho . O que ele escreveu geometria em causa e há várias idéias deste trabalho inédito que estavam à frente de seu tempo , tais como : noções de invariância topológica.

Além de seu trabalho em geometria, Bolyai desenvolveu um conceito geométrica rigorosa dos números complexos como pares ordenados de números reais. Isso ele fez Jablonowsky porque a sociedade em Leipzig tinha colocado uma chamada de trabalhos sobre o tema. Ambos Bolyai e seu pai apresentou documentos , mas não foram bem recebidos. O trabalho de János foi chamado Responsio e foi escrito para responder à questão de saber se as quantidades imaginárias utilizadas em geometria poderia ser construído. Bolyai que escolheu para discutir a questão foi mal formulada , talvez não seja a melhor maneira de encontrar favor com os juízes . Ele argumentou que não era que a sua construção Isso era importante , era sim a sua definição e seu papel na geometria que foram significativas.

Em 1846 mudou-se Bolyai do verão em Domald para Marosvásárhely . Esta Isso significava que ele estava mais perto de Seu Pai e isso parecia tornar as relações entre os dois tensas mesmo amoras . Em 1848, Bolyai descoberto que Lobachevsky tinha publicado um pedaço de trabalho semelhante em 1829. Kagan escreve [ 14] : -

János estudou a obra de Lobachevsky cuidado e Analisados ​​linha por linha , palavra por palavra não quer dizer, com tanto cuidado como ele administrou a trabalhar no apêndice . O trabalho provocou uma verdadeira tempestade em sua alma e deu saída para suas tribulações nos comentários adicionados dos Exames geométricas ".

Os 'Comentários' para o ' Exames geométrica ' são mais do que uma análise crítica do trabalho . Eles expressam os pensamentos e angústias dos János provocadas pela leitura do livro. Incluem sua queixa de que ele foi injustiçado, sua suspeita de que Lobachevsky não existem, e que tudo foi o rancoroso maquinações de Gauss : é o trágico lamento de um geômetra engenhoso que estava ciente do significado de sua descoberta , mas não conseguiu obter o apoio da única pessoa que poderia ter apreciado seus méritos .

Apesar de sua agitação mental em meio à qual János observações colocadas no papel , ele preservou o suficiente objetividade aprecio muito o trabalho do seu rival. Em seu comentário ao Teorema 35 Que observações sobre as provas de Lobachevsky trigonometria esférica urso a impressão de genialidade e seu trabalho deve ser respeitado como uma conquista magistral .

Em 1852 Bolyai esquerda Rozália , - com quem se casou em 18 de maio de 1849 acreditando que a lei agora mudou para os dois Hungatian declaração de independência, e dividir com Rozália pelo menos teve a vantagem de que a melhoria das relações com seu pai . Ele desistiu de trabalhar a matemática em seus últimos anos e em vez disso tentou construir uma teoria de todo o conhecimento . Há idéias interessantes contidas nas seções sobre lingüística e sociologia.

Apesar de nunca ter publicado mais do que as poucas páginas do Apêndice deixou mais de 20 mil páginas do manuscrito de trabalho matemático Quando Ele morreu de pneumonia na idade de 57 . Estes são agora na biblioteca Bolyai - Teleki em Tirgu - Mures . Em 1945 universidade em Cluj foi nomeado depois dele, mas foi fechado pelo governo de Ceausescu em 1959.

A imagem dele é tirado de um selo emitido pelos Correios húngaro para celebrar o centenário de sua morte. Não se acredita ser autêntico e não existe autêntica da imagem .


Artigo por: J O'Connor e Robertson E F

mar 2004

ARTE MATEMÁTICA (42)

Vários hexágonos foram construídos um dentro do outro. Perceba o efeito obtido.

MATEMÁGICA? (42)

Pegue uma calculadora e faça as operações abaixo.
Antes porém, lembre-se de que deve fazer as multiplicações e as potências antes das somas e das subtrações...

    6² - 3 x 12 = 
    7² - 4 x 12 = 
    8² - 5 x 12 = 
    9² - 6 x 12 = 
  10² - 7 x 12 = 
  11² - 8 x 12 = 
  12² - 9 x 12 =
13² - 10 x 12 =
14² - 11 x 12 =
15² - 12 x 12 =
16² - 13 x 12 =

Então? Percebeu que números são estes que apareceram nas respostas???

Tente estas outras:


    3² - 2 x 4 = 
    4² - 3 x 4 =
    5² - 4 x 4 =
    6² - 5 x 4 =
    7² - 6 x 4 =
    8² - 7 x 4 =
    9² - 8 x 4 =
  10² - 9 x 4 =
11² - 10 x 4 =
12² - 11 x 4 =

Que tal?!?